January 13th, 2016
Using DFA for Wildcard Matching Problem
Wildcard matching has a very simple matching language: use “?” to match any single character and “*” for matching any text (include empty). It is not as powerful as regular expression, but on the other side it is much more understandable for the end user. Some examples:
| text | pattern | matchs |
|---|---|---|
| aa | a | no |
| aa | aa | yes |
| aaa | aa | no |
| aa | * | yes |
| aa | a* | yes |
| ab | ?* | yes |
| aab | c*a*b |
yes |
Recently I need implement it for one of my side project. In the project most user search goes through lucene index query NEO4j embedded when doing a wildcard match. But in some cases when user’s search cannot directly map to a index, I need go through large amount of strings to find matches.
It is a interesting algorithm problem not as simple as it looked like. Because "*" match needs greedily look forward. For example, in the case of “abcbc” matching pattern “a*bc”, the algorithm need backtrack to "*" to restart matching when it found “abcb” do not match “a*bc”.
Start with a naive implementation
I happened to solve this problem on leetcode long time ago. At the time I wrote a naive implementation based on recursive backtracking. Once encounter a "*", the algorithm scan from back of the text, and try recursively find a match for rest of the patten. This algorithm can handle greedy cases like (“abcbb”, “a*bc”) correctly, but yield very high time complexity. If text length is n, and pattern length is m, the worst case complexity is O(n!*m). So the algorithm never finish when text is long and pattern has a lot of stars, such as:
pattern: "a*b*a*b*aaaa*abaaa**b*a***b*a*bb****ba*ba*b******a********a**baba*ab***a***bbba*b**a*b*ba*a*aaaa*ab"
text: "aabbbbaababbabababaabbbbabbabbaabbbabbbabaabbaaaababababbababbabbbbabaaabaaabaabbaaaabbbbabaaabbbbbabbbaabbbbbabaabababaaabaaababaababbaaabaabbabaababbabababaaababbabbabaabbbbabbbbabaabbaababaaabababbab"At the time I ended up with putting a cache for failures matches. It helped shortcut the factorial part and reduce the worst case complexity to O(n*m). Good enough for me to move on.
Lucene’s implementation
But this obviously is not good enough for production code. I was wondering what is Lucene’s implementation looked like. So I download source code of Lucene 3.6.2. (v3.6.2 is the version of Lucene that Neo4j embedded). I was shockingly surprised the implementation is almost identical to my first naive implementation. It does not even have the failure caches so it is a straight worst case O(n!*m) algorithm. I guess this means if you find some server software using Lucene 3 and you can make a wildcard query, you can easily DOS it using previous mentioned cases.
(I have already check latest version of Lucene. Turns out from version 4.0, Lucene switched to a DFA solution. So there is no need to race for a pull request :-).
Solution based on DFA
This problem is somehow similar with classic “find needle in the hay” string searching problem. For that we have the famous KMP algorithm. KMP is inspiring on how it compiles the pattern into a lookup table to so that it only need go through the text string once without backtracking. In our cases, because we need go though large amount of strings, it will be really beneficial if we can compile pattern to some kind of structure helping us scan the text only once. It will make the worst time complexity of each match to O(n).
The most straight forward helpful structure we can compile to is a FSM (Finite-state machine). More specificly a DFA (Deterministic finite state machine). With it we can present each matching situations via states, from each state we can use transitions tells which state it should switch to base on the current character read. For example, we can present the pattern a*bc as following state machine:
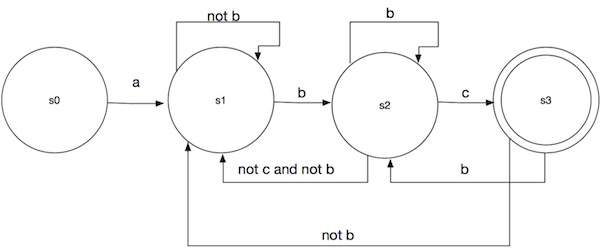 
In this state machine, s0 is initial state presenting match no input. State s3 is the accepting state (denoted by double circle). The matching process become: start from s0, base on the input character following the corresponding transition transit to the next state. Keep doing this until there is no transition to go (dead end return not match), or reaching the end of the text. In later case return “match” if the machine stops at a acceptable state (s3 in our case) otherwise “no match”.

In this state machine, s0 is initial state presenting match no input. State s3 is the accepting state (denoted by double circle). The matching process become: start from s0, base on the input character following the corresponding transition transit to the next state. Keep doing this until there is no transition to go (dead end return not match), or reaching the end of the text. In later case return “match” if the machine stops at a acceptable state (s3 in our case) otherwise “no match”.
Here is an example:
text: abcbc
pattern: a*bc
read ‘a’, s0 -> s1
read ‘b’, s1 -> s2
read ‘c’, s2 -> s3
read ‘b’, s3 -> s2
read ‘c’, s2 -> s3
read EOF, s3 is acceptable state, return matchYou can verify it with different input yourself. It works correctly and you should be able to get a concrete feeling on how the matching works.
Building this state machine is a reasonable task. But it is kind of tedious to do. Fortunately there are state machine libraries available allowing define state machine with high level declarations. The library I used is dk.brics.automaton. Here is the java code to create the state machine:
public static Automaton toAutomaton(String pattern) {
Automaton automaton = Automaton.makeEmptyString();
for (int i = 0; i < pattern.length(); i++) {
char p = pattern.charAt(i);
switch (p) {
case '*':
automaton = automaton.concatenate(Automaton.makeAnyString());
break;
case '?':
automaton = automaton.concatenate(Automaton.makeAnyChar());
break;
default:
automaton = automaton.concatenate(Automaton.makeChar(p));
}
}
return automaton;
}Java matching code using the DFA:
public static boolean wildcardMatch(String text, Automaton automaton) {
return automaton.run(text);
}Now we have a super simple O(n) implementation for each single matches.